Seasonal ARIMA analysis 5.0
Summary
This operator creates a seasonal ARIMA model for time-related observations. A forecast is created with the help of this model.
In time series analysis, an autoregressive integrated moving average (ARIMA) model is a generalization of an autoregressive moving average (ARMA) model. These models are fitted to time series data either to better understand the data or to predict future points in the series (forecasting). They are applied in some cases where data show evidence of non-stationarity, where an initial differencing step (corresponding to the "integrated" part of the model) can be applied to reduce the non-stationarity (wikipedia).
Configuration
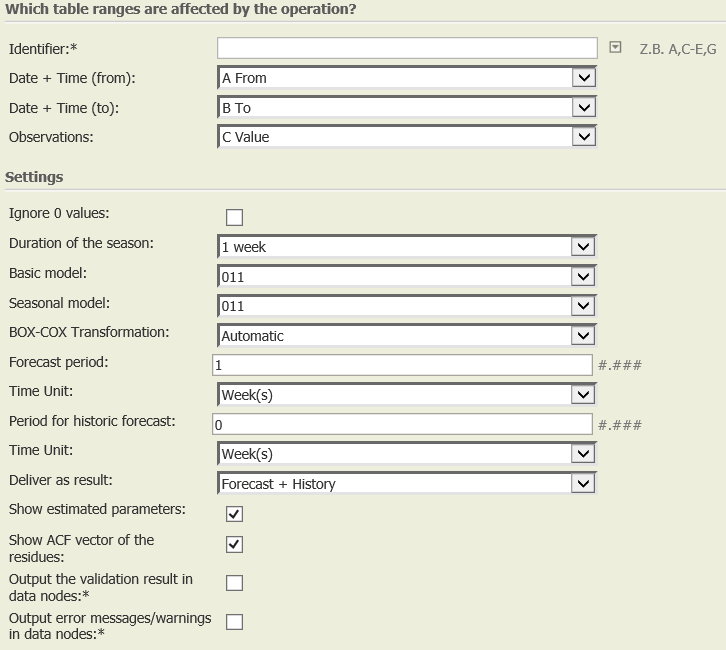
Input settings of existing table
Name | Value | Opt. | Description | Example |
|---|---|---|---|---|
Identifier | System.Object | opt. | Please select those columns based upon whose content the data should be grouped. A separate seasonal ARIMA analysis will be conducted for each group. | - |
Date + Time (from) | System.DateTime | - | Please select the column that contains the start times (date + time) of your observations. | - |
Date + Time (to) | System.DateTime | - | Please select the column that contains the final times (date + time) of your observation. | - |
Observations | System.Double | - | Please select the column which contains the observations relevant for the seasonal ARIMA analysis. | - |
Settings
Name | Value | Opt. | Description | Example |
|---|---|---|---|---|
Ignore 0 values | System.Boolean | - | Rows with 0-values are ignored in the seasonal ARIMA model and are treated like missing data. | - |
Duration of the season | System.String
| - | Please enter the duration of the season (=number of the data/observations/values of a season). The duration of the season must be equal to or greater than one. | - |
Basic model | System.String
| - | Please select the type of ARIMA process for the basic model. A model that can be applied to a great deal of data is a basic model=011, seasonal model=011. This model corresponds to the Holt winter seasonal method. | - |
Seasonal model | System.String
| - | Please select the type of the ARIMA process for the seasonal model. A model that can be applied to many kinds of data is basis model=011, seasonal model=011. This model corresponds to the Holt winter seasonal method. | - |
@BOXCOXTRANSFORMATION | System.String
| - | The BOX-COX transformation transforms the observations into a form that can be used for the seasonal ARIMA analysis. If you select 'automatic' as the type of BOX-COX transformation, a transformation suitable for the data on which the analysis is based is defined. Another type of transformation should then only be used if you have sound knowledge of the data to be analysed. Select '1 (identity)', if the seasonal variations remain absolutely constant, e.g. the December value is always 1000 units higher than the annual average. Select '0 (logarithm)', if the seasonal variations are a constant percentage, e.g. the December value is always 20% higher than the annual average. Select '0.5 (root)', if the seasonal variations are a constant percentage, but the percentage reduces slightly over time, e.g. the first December value is 20% higher than the monthly average, the second December value is 19% higher, etc. Select '-1 (reciprocal)' for non-negative data with falling trend, for example, as for sales data from a bookshop/publishers, where high figures are observed for the first few months after publication, but then gradually reduce over time. | - |
Forecast period | System.Int32 | - | Please enter the period, e.g. the next 6 weeks, for which a forecast is to be calculated. | - |
Time Unit | System.String
| - | Please enter the period, e.g. the next 6 weeks, for which a forecast is to be calculated. | - |
Period for historic forecast | System.Int32 | - | Please enter the period, e.g. the last 6 weeks, for which a historical forecast is to be calculated. | - |
Time Unit | System.String
| - | Please enter the period, e.g. the last 6 weeks, for which a historical forecast is to be calculated. | - |
Deliver as result | System.String
| - | Please select which data should be displayed in the results. | - |
Show estimated parameters | System.Boolean | - | If selected, the following estimated parameters of the seasonal ARIMA model will be displayed: Lambda (BOX-COX transformation), AR-basis, MA-basis, AR-season, MA-season. | - |
Show ACF vector of the residues | System.Boolean | - | If selected, the estimated vector of the auto-correlation function of the residues will be displayed (Lag 1 - Lag 25). | - |
Output the validation result in data nodes | System.Boolean | - | If selected, the validation results are displayed in a separate data node. | - |
Output error messages/warnings in data nodes | System.Boolean | - | If selected, error messages and warnings are displayed in a separate data node. | - |
Want to learn more?
Screenshot
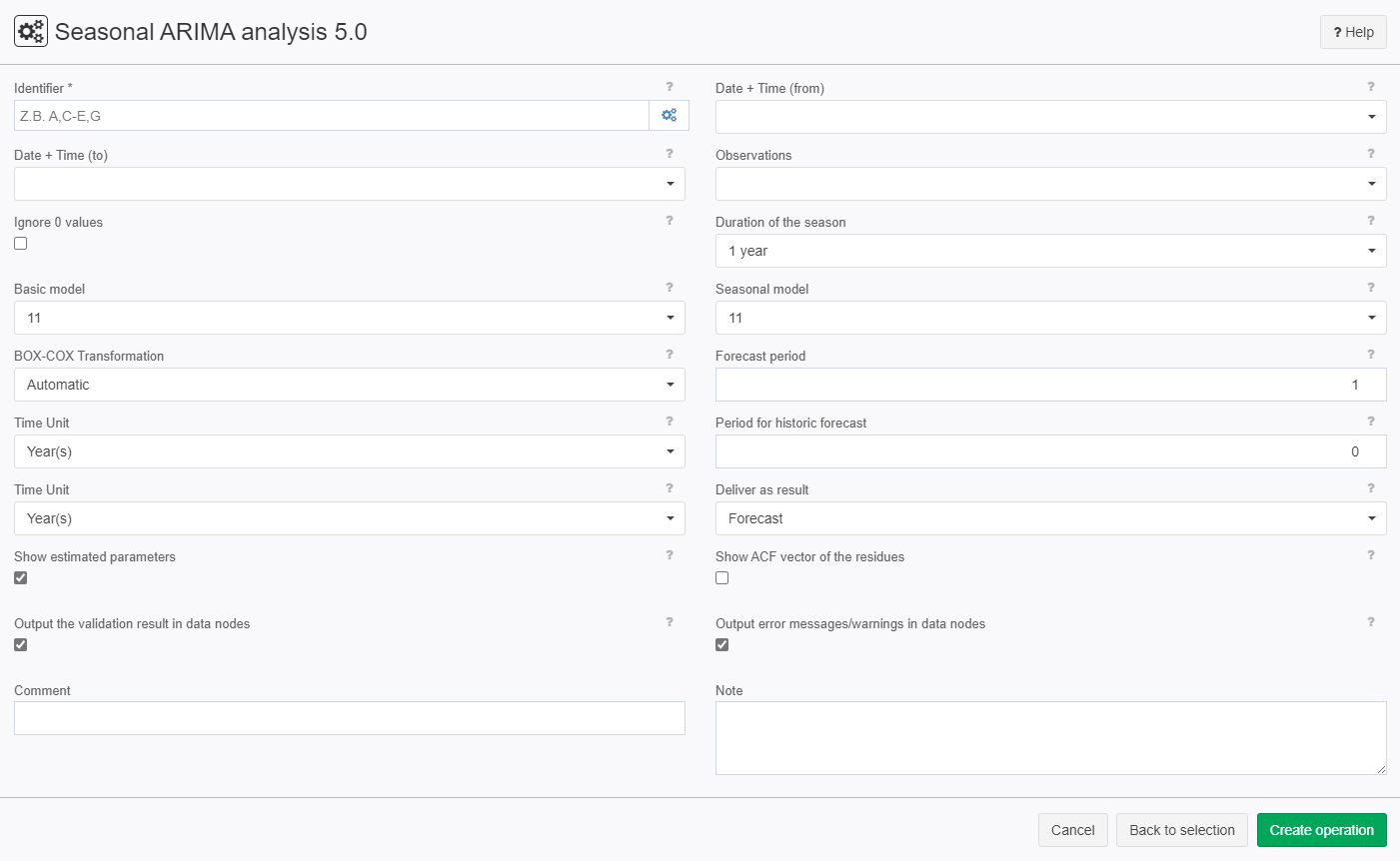
This operator creates a seasonal ARIMA model for time-related observations. A forecast is created with the help of this model.
More detailed information
Data requirements
- Input data always need to be sorted by time stamps in column "Date + time". SARIMA Analysis cannot be conducted if this is not the case.
- There always need to be 1 season + 1 observation to conduct SARIMA analysis. It does not make sense to calculate a SARIMA model with less data.
- Missing time stamps in the input data will be completed as missing rows and treated as missing observations.
Using SARIMA
The TIS-GUI and the SARIMA operator description provide additional information and (if necessary) warnings.
- To calculate an ARIMA analysis without seasonality, please choose 000 as seasonal model and 1 as duration of the season.
- Days known to be 0 (e.g., Sundays in retail) should be excluded BEFORE from the time series data.
Statistical info
- It is difficult to calculate several periods into the future. If you want to forecast further, calculate on an aggregated level (e.g., with weeks instead of days). This will have the disadvantage of losing information, though.
- For some data it makes sense to use Autoregression = 2 or Moving Average = 2. However, this leads to slow parameter estimation and rarely provides much better forecasts. Therefore, these models are not provided in TIS at the moment. They can, however, be provided on demand.
- Hint: Random Walk = AR1 processes with coefficient 1; this means: the basic model 010 without seasonality. Since no parameter needs to be estimated in the random walk model, and forecast is simply the last observation, this model cannnot directly be chosen. A random walk modell can be estimated by chosing e.g. basic model 011 and seasonal model 000, and the estimated parameter is very close to 0.
- Autocorrelation function of residuals = ACF Auto Correlation Function
- e.g. Value = 0.7 ... shows that the model does not fit
- e.g. ABS(x) <0.15 indicates a good model
- Parameter estimation in TIS is based on MLE (Maximum Likelihood Estimation)
Examples
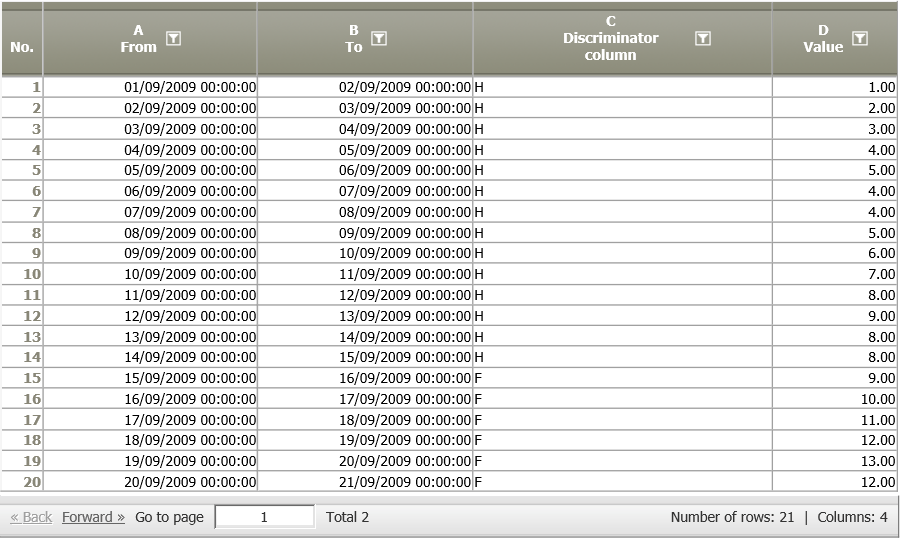
Example: Estimating a SARIMA model
Situation | A value is measured across 14 days. The data show that the value increases by 1 each day and decreases by 1 on the seventh day.
|
|---|---|
Settings |
|
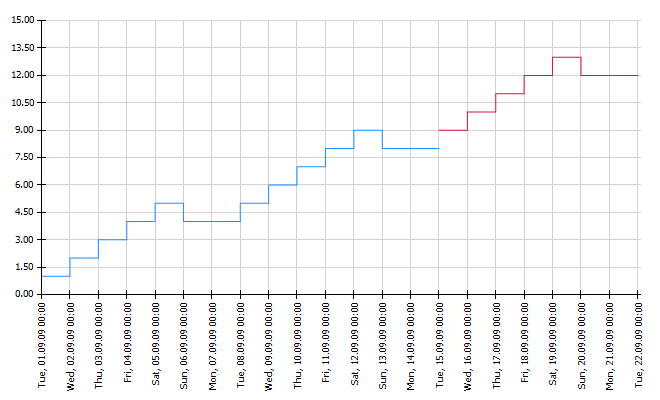
Result |
The operator settings show also the parameter estimates for Lambda (BOX-COX Transformation), coefficients for AR- and MA-processes of the basic and seasonal model. Additionally, the estimated ACF vector of the residues is shown.
To visualize the results, e.g., in a chart, please add a new data node with the operation Chart: Histogram Time Pattern. The result will look similar to the chart below.
|
Project-File |
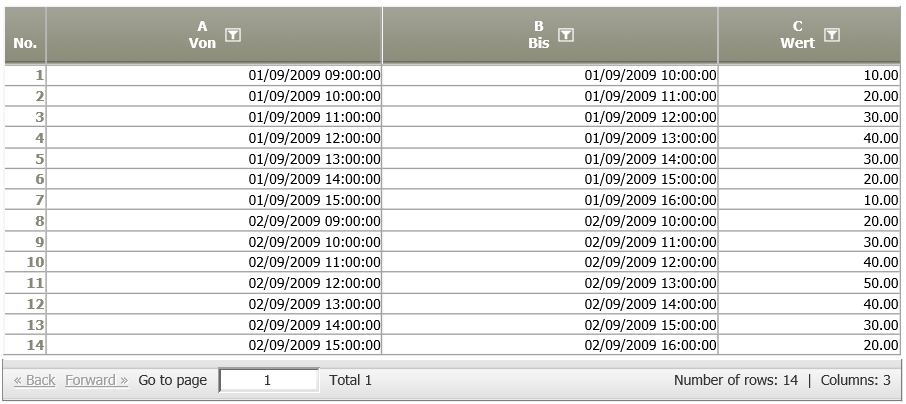
Example: SARIMA model with hourly interval data
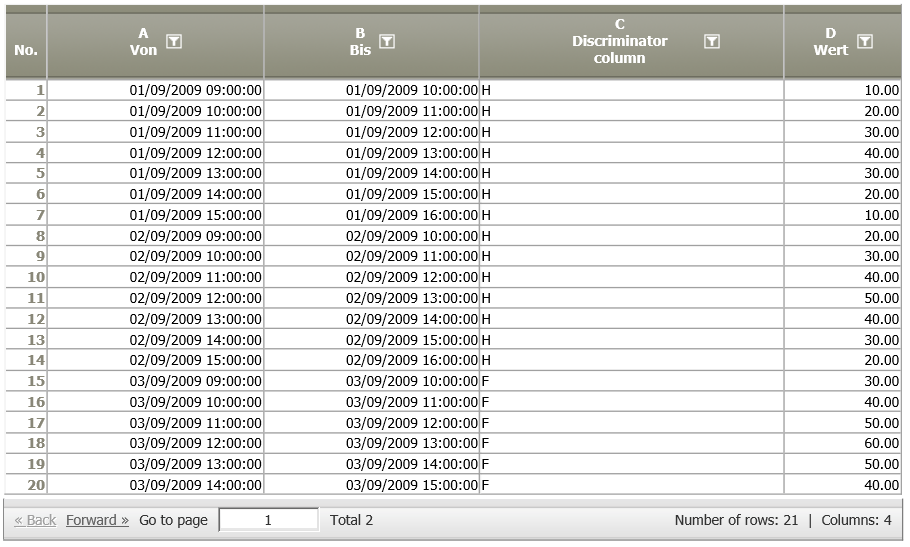
Situation | On two subsequent days, a value is measured each hour in the time between 09:00 to 15:00 hours.
|
|---|---|
Settings |
|
Result |
The operator settings show also the parameter estimates for Lambda (BOX-COX Transformation), coefficients for AR- and MA-processes of the basic and seasonal model. Additionally, the estimated ACF vector of the residues is shown.
|
Troubleshooting
Problem | Frequent Cause | Solutions |
|---|---|---|
Error message, or "n. def." | The error can be caused by the raw data of the combination of identifiers. E.g., there are too few values to calculate a certain figure. | Create larger groups, i.e., less filtering by identifier instances. |